Feel free to let the visitors explore the tiles on their own and see what combinations will tessellate.

Participants may enjoy trying to put together groups of 6 monkey magnets in different ways, but point out to them that each of these ways is part of a single larger tessellation pattern, which they can see on the mat. Note that the monkeys are brittle and may crack if dropped, so discourage horseplay. Monkey magnets are available for sale in MoMath's online shop.

1. Find a way to tessellate using only squares. Then use only hexagons. Then use only triangles.
2. • Other than the usual the square grid, can they find another tessellation using just squares? (Yes. They can slide rows over.)
   • Besides the usual hexagonal packing, can they find another tessellation using only hexagons? (No.)
   • With triangles? (Yes. Again, slide rows over.)
3. Can they tessellate using two of the three polygons? (Squares and triangles: yes. Triangles and hexagons: yes. Squares and hexagons: no.)
4. Can they tessellate using all three together: squares, triangles, and hexagons? (Yes.)
5. Can they find tessellations for (1)-(4) where each vertex looks the same? (Yes.)

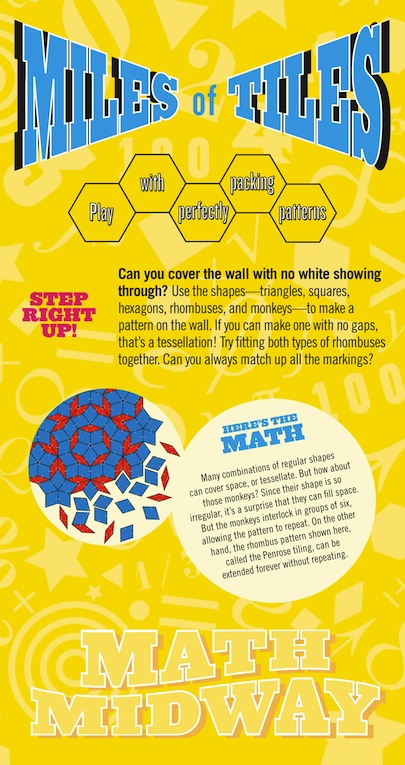
With the rhombic tiles, there are many ways to tessellate if you ignore the printed markings. If you match up the printed markings, as shown on the sandwich board, then the resulting tessellation will be the aperiodic "Penrose tiling". No two large regions of this tiling will be the same -- it does not repeat.